Un poligon \(P_1 P_2 \dots P_n P_1\) se numește stelat dacă există un punct \(M\) în interiorul său astfel încât, oricum s-ar alege un punct \(X\) pe laturile poligonului sau un vârf al acestuia, segmentul \([MX]\) este conținut în întregime în interiorul poligonului.

Fiind dat un poligon stelat, trebuie să implementați un algoritm cu complexitate liniară de timp care să găsească acoperirea convexă a unui poligon stelat.

Date de intrare

Se va citi de la tastatură un număr \(n\), reprezentând numărul de vârfuri al poligonului și apoi \(n\) linii care conțin perechi de numere întregi \(x_i \ y_i\), separate prin spațiu, reprezentând coordonatele vârfului \(P_i\), parcurse în sens trigonometric.

Date de ieșire

Programul va afișa un număr \(k\), reprezentând numărul de vârfuri ale acoperirii convexe a mulțimii \({ P_1, P_2, \dots, P_n }\) și apoi \(k\) perechi de numere întregi, pe linii distincte, reprezentând coordonatele acestor vârfuri, parcurse tot în sens trigonometric (dar puteți porni de la orice vârf).

Restricții și precizări

• \(1 \leq n \leq 100\,000\)
• \(-10^9 \leq x_i, y_i \leq 10^9\)

Exemple

Exemplul 1

Input

3
-1 3
-3 -2
4 -3

Output

3
-1 3
-3 -2
4 -3

Explicație

Exemplul corespunde următorului poligon stelat, un triunghi oarecare:

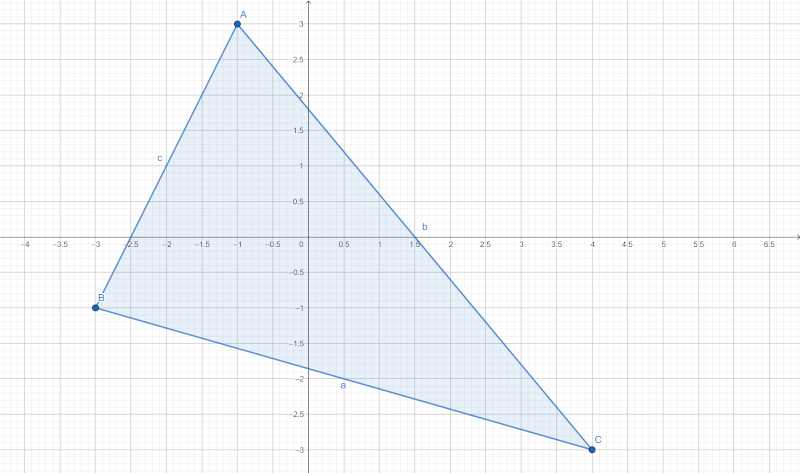
Puteți începe să descrieți acoperirea convexă de la orice vârf al ei, cât timp parcurgerea este în sens trigonometric. \((-3, 2), (4, -3), (-1, 3)\) și \((4, -3), (-1, 3), (-3, 2)\) erau de asemenea soluții acceptabile.

Exemplul 2

Input

10
0 3
-1 1
-5 0
-2 -1
-4 -5
1 -2
5 -3
3 0
6 3
2 2

Output

5
-4 -5
5 -3
6 3
0 3
-5 0

Explicație

Exemplul corespunde următorului poligon stelat, o stea neregulată cu 5 colțuri:

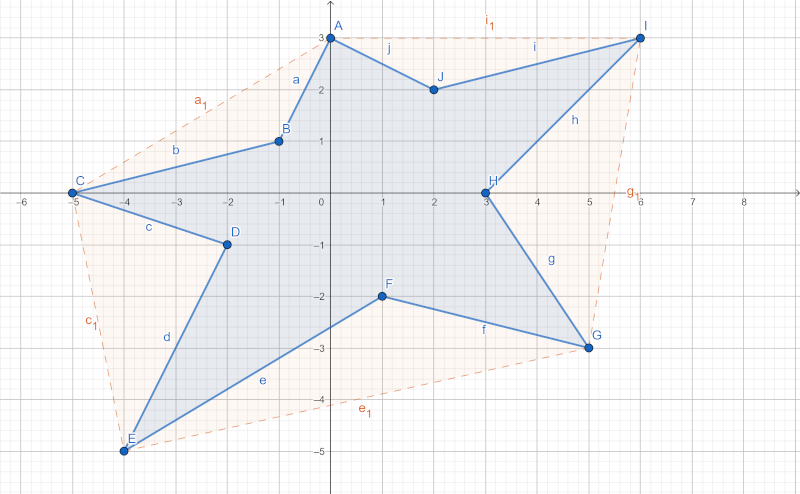
Exemplul 3

Input

8
0 2
-2 2
-2 0
-2 -2
0 -2
2 -2
2 0
2 2

Output

4
-2 2
-2 -2
2 -2
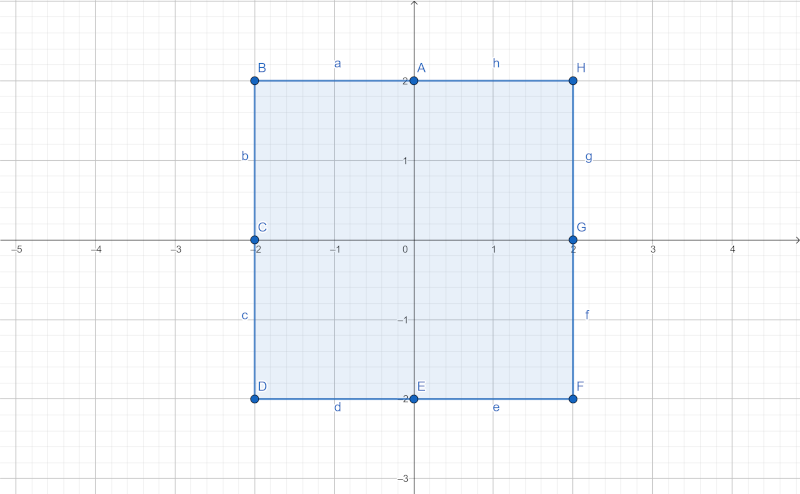
2 2

Explicație

Exemplul dat este o stea cu 4 colțuri degenerată, care e de fapt un pătrat: