Descriere

Implementați algoritmul care construiește, în context euclidian, un traseu optim pentru Travelling Salesman Problem folosind acoperirea convexă (acesta este descris aici).

Date de intrare

Se vor citi de la tastatură \(n\), numărul de puncte din plan, și apoi \(n\) perechi de numere întregi \(x_i, y_i\), reprezentând coordonatele punctelor.

Date de ieșire

Se vor afisa pe ecran vârfurile unui ciclu hamiltonian de cost minim, primul vârf din ciclu fiind cel cu abscisa minimă.

Restricții și precizări

• \(3 \leq n \leq 1\,000\).
• \(-1\,000 \leq x_i, y_i \leq 1\,000\)
• Pentru această problemă nu se pot trimite rezolvări în Python, deoarece acestea ar depăși pe unele teste limita de timp impusă de platformă.

Exemplu

Input

10
6 10
0 5
4 -7
3 8
3 -8
-4 -2
-10 -1
0 -9
4 -3
-7 10

Output

-10 -1
-4 -2
0 -9
3 -8
4 -7
4 -3
6 10
3 8
0 5
-7 10
-10 -1

Explicație

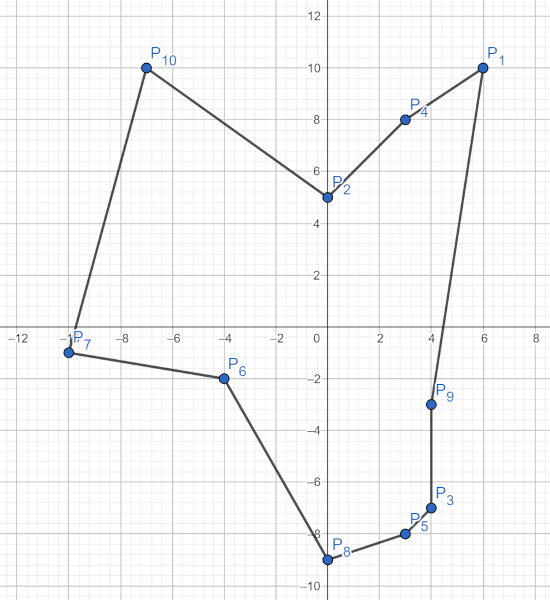
Mulțimea de puncte din exemplu arată în felul următor:

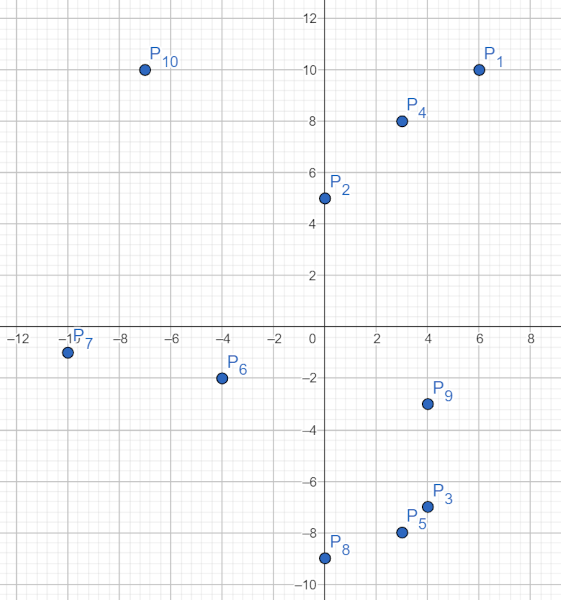
Înfășurătoarea convexă a punctelor este următorul poligon convex:

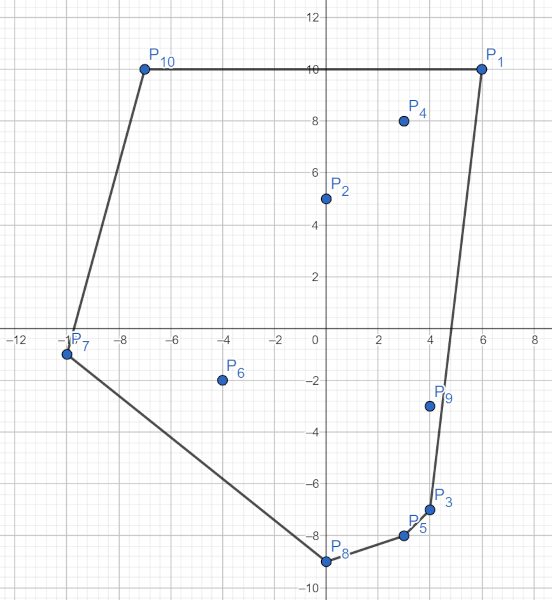
Aplicând algoritmul menționat, se obține următoarea soluție: