Descriere

Se consideră un poligon convex cu \(n\) vârfuri date în ordine trigonometrică (\(P_1 P_2 \dots P_n\)) și \(m\) puncte în plan (\(R_1, R_2, \dots, R_m\)). Pentru fiecare dintre cele \(m\) puncte să se stabilească dacă se află în interiorul, în exteriorul sau pe una dintre laturile poligonului.

Date de intrare

Se citește de la tastatură \(n\), reprezentând numărul de vârfuri ale poligonului. Următoarele \(n\) linii vor conține câte două numere întregi \(x_i, y_i\), coordonatele punctului \(P_i\).

Pe următoarea linie se află \(m\) reprezentând numărul de puncte pentru care trebuie să aflăm poziția față de poligon. Următoarele \(m\) linii vor conține câte două numere întregi \(x_i, y_i\), coordonatele punctului \(R_i\).

Date de iesire

Pentru fiecare punct \(R_i\) se va afișa, pe câte un rând nou, un mesaj corespunzător poziției sale față de poligon:

• INSIDE (dacă punctul \(R_i\) se află în poligon)
• OUTSIDE (dacă punctul \(R_i\) se află în afara poligonului)
• BOUNDARY (dacă punctul \(R_i\) se află pe una dintre laturile poligonului)

Restricții și precizări

• \(3 \leq n, m \leq 10^5\).
• \(-10^9 \leq x_i, y_i \leq 10^9\)

Exemplu

Input

4
0 0
5 0
5 5
0 5
3
2 2
7 7
5 2

Output

INSIDE
OUTSIDE
BOUNDARY

Explicație

Reprezentarea grafică a situației de mai sus este următoarea:

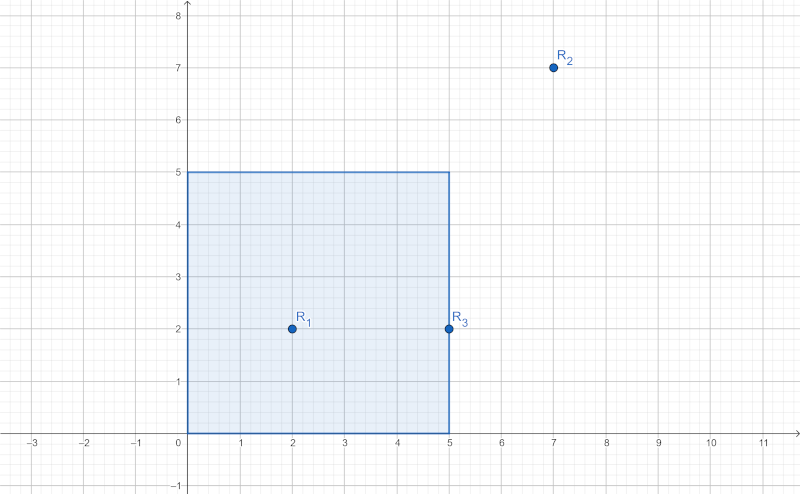
Indicații de rezolvare

O metodă simplă de a verifica dacă un punct se află în interiorul unui poligon convex este descrisă aici și se bazează pe efectuarea testului de orientare între fiecare latură a poligonului convex și punctul ales. O astfel de verificare necesită \(\mathcal{O}(n)\) timp, deci per total soluția are complexitatea-timp \(\mathcal{O}(mn)\).

Pentru a trece toate testele, trebuie să implementați o soluție care să ruleze în timp \(\mathcal{O}(m \log n)\). Un astfel de algoritm, care utilizează o căutare binară, este descris pe acest site.