Descriere

Implementați un algoritm de complexitate de timp liniară care să determine poziția relativă a unui punct \(Q\) față de un poligon arbitrar \(P_1, \dots, P_n\).

Date de intrare

Programul va citi de la tastatură un număr natural \(n\) și apoi \(n\) perechi de numere întregi separate prin spațiu \(x_i \, y_i\), pe linii distincte, reprezentând coordonatele vârfului \(P_i (x_i, y_i)\) al poligonului.

După aceea urmează numărul natural \(m\) și apoi \(m\) perechi de numere întregi separate prin spațiu \(x_j \, y_j\), reprezentând coordonatele punctului \(Q_j (x_j, y_j)\).

Date de ieșire

Pentru fiecare dintre cele \(m\) puncte, programul va afișa pe ecran:

• INSIDE: dacă punctul \(Q_j\) se află în interiorul poligonului;
• OUTSIDE: dacă punctul \(Q_j\) se află în exteriorul poligonului;
• BOUNDARY: dacă punctul \(Q_j\) se află pe laturile poligonului.

Restricții și precizări

• \(3 \leq n \leq 1000\)
• \(1 \leq m \leq 1000\)
• \(-10^9 \leq x, y \leq 10^9\)

Exemplu

Input

12
0 6
0 0
6 0
6 6
2 6
2 2
4 2
4 5
5 5
5 1
1 1
1 6
3
3 4
7 3
3 2

Output

INSIDE
OUTSIDE
BOUNDARY

Explicație

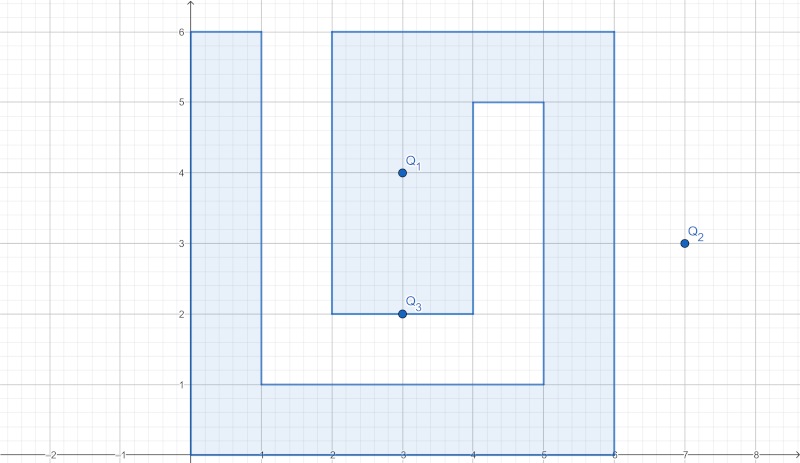
Reprezentarea grafică a situației de mai sus este:

Indicații de rezolvare

Varianta 1 (O soluție incompletă, care permite obținerea unui punctaj parțial)

Puteți folosi problema 1 de la acest laborator, care rezolvă cerința în cazul poligoanelor convexe. Combinând cu soluția problemei 3 de la L5, se ajunge la o soluție în cazul poligoanelor stelate.

Varianta 2 (O soluție completă, bazată pe o abordare diferită)

Soluția completă se bazează pe regula "par-impar" ("odd-even rule"), principiu folosit pentru a delimita interiorul unui poligon sau al unei linii poligonale cu autointersecții. Numele de "par-impar" derivă din următorul mecanism (descris pe scurt):

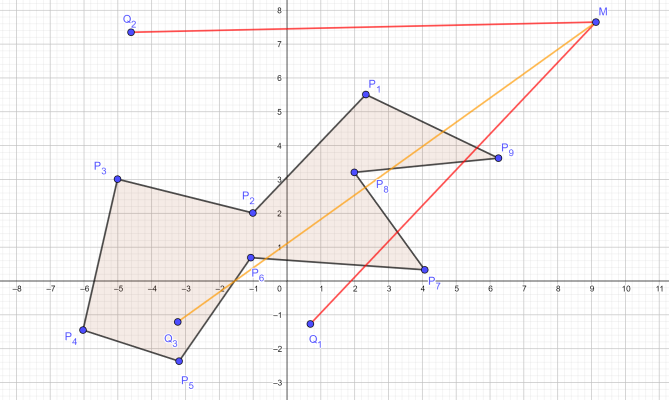
• Se alege un punct \(M\) "departe" de poligon (de exemplu coordonatele lui \(M\) să fie mai mari / mai mici decât coordonatele corespunzătoare ale tuturor vârfurilor poligonului).
• Se determină numărul de laturi intersectate de segmentul deschis \((MQ)\) în interior. Dacă acest număr este par, punctul \(Q\) este situat în exteriorul poligonului, iar dacă este impar, punctul este situat în interior.
• O implementare completă trebuie să trateze corect cazul în care punctul \(Q\) este situat pe una din laturile poligonului. De asemenea, dacă segmentul \((MQ)\) trece printr-un vârf al poligonului, trebuie ales un alt punct "departe" de poligon. Se demonstrează că numărul total de intersecții se poate modifica, dar paritatea rămâne neschimbată.
• În exemplul din figură, pentru punctele \(Q_1\) și \(Q_2\), numărul de intersecții dintre segmentele \((MQ_1)\), respectiv \((MQ_2)\) este par (4, respectiv 0), punctele fiind situate în exteriorul poligonului. Pentru punctul \(Q_3\), numărul de intersecții este impar (5), punctul fiind situat în interiorul poligonului.

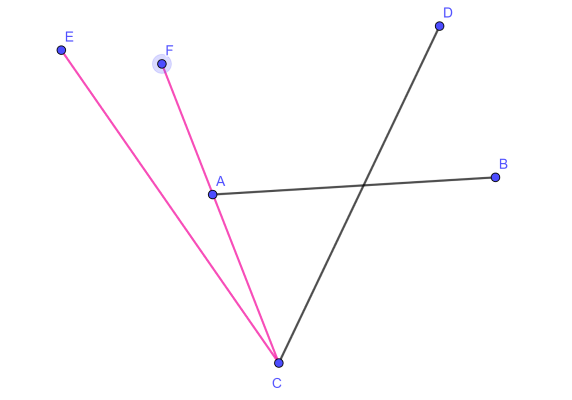
• Două segmente deschise \((AB)\) și \((CD)\) se intersectează în interior dacă și numai dacă \(A\) și \(B\) sunt de o parte și de alta a dreptei \(CD\) și \(C\) și \(D\) sunt de o parte și de alta a dreptei \(AB\). Aceste proprietăți se verifică aplicând testul de orientare.

• În figura de mai jos, segmentele deschise \((AB)\) și \((CD)\) se intersectează, fiind verificată proprietatea de mai sus. Observați că segmentele \((AB)\) și \((CE)\) nu se intersectează. Astfel, \(C\) și \(E\) sunt de o parte și de alta a dreptei \(AB\), dar \(A\) și \(B\) nu sunt de o parte și de alta a dreptei \(CE\). De asemenea, segmentele deschise \((AB)\) și \((CF)\) nu se intersectează (\(A\) este situat pe dreapta \(CF\), deci \(A\) și \(B\) nu pot fi de o parte și de alta a dreptei \(CF\)).